確定一個(gè)子串(模式串)在主串中第一次出現(xiàn)的位置。
BF算法(Brute-Force算法)
BF算法即樸素的簡單匹配法,采用的是窮舉的思路。從主串的每一個(gè)字符開始依次與模式串的字符進(jìn)行比較。

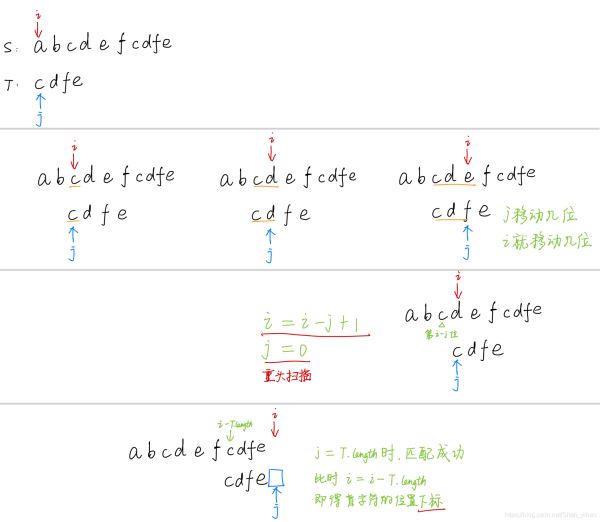
int index_BF(SeqString S, SeqString T, int begin)//從S的第begin位(下標(biāo))開始進(jìn)行匹配判斷
{
int i = begin, j = 0;
while (i < S.length && j < T.length)
{
if (S.ch[i] == T.ch[j])
{
i ++;
j ++;//比較下一個(gè)字符
}
else
{
i = i - j + 1;
j = 0;//模式串回溯到起點(diǎn)
}
}
if (j == T.length) return i - T.length; //匹配成功,則返回該模式串在主串中第一次出現(xiàn)的位置下標(biāo)
else return -1;
}
int index_BF(char S[], char T[], int beg)
{
int i = beg, j = 0;
while (i < strlen(S) && j < strlen(T))
{
if (S[i] == T[j])
{
i ++;
j ++;
}
else
{
i = i - j + 1;
j = 0;
}
}
if (i == strlen(S)) return i - strlen(T);
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "cde";
printf("%d", index_BF(str1, str2, 0));
return 0;
}
KMP算法(快速的)
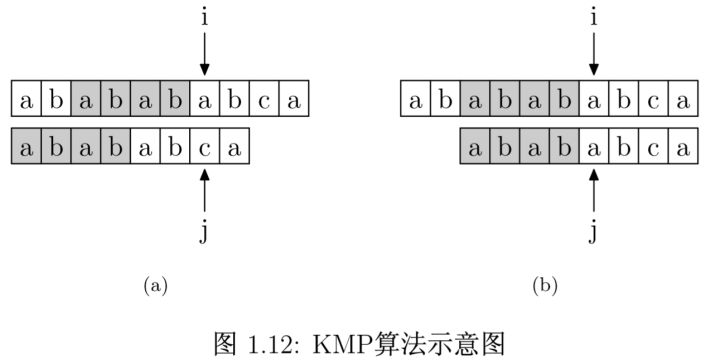
基本思想為:主串的指針 i i i不必回溯,利用已經(jīng)得到前面“部分匹配”的結(jié)果,將模式串向右滑動若干個(gè)字符,繼續(xù)與主串中的當(dāng)前字符進(jìn)行比較,減少了一些不必要的比較。
時(shí)間復(fù)雜度為 O ( n + m )
KMP算法的核心,是一個(gè)被稱為部分匹配表(Partial Match Table)的數(shù)組。
首先要明白什么是字符串的前綴和后綴。
如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就稱B為A的前綴。例如,”Harry”的前綴包括{”H”, ”Ha”,”Har”, ”Harr”},我們把所有前綴組成的集合,稱為字符串的前綴集合。
同樣可以定義后綴A=SB,其中S是任意的非空字符串,那就稱B為A的后綴,例如,”Potter”的后綴包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后綴組成的集合,稱為字符串的后綴集合。
要注意的是,字符串本身并不是自己的前綴或后綴。
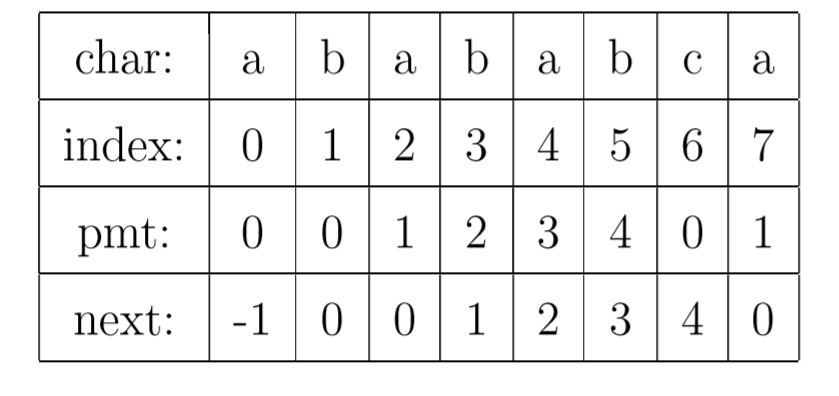
PMT中的值是字符串的前綴集合與后綴集合的交集中最長元素的長度。
比如,對于字符串”ababa”,它的前綴集合為{”a”, ”ab”, ”aba”, ”abab”},它的后綴集合為{”baba”, ”aba”, ”ba”, ”a”}, 兩個(gè)集合的交集為{”a”, ”aba”},其中最長的元素為”aba”,長度為3,即該字符串在PMT表中的值為3。性質(zhì)為:該字符串前3個(gè)字符與后三個(gè)字符相同。
如果模式串有 j個(gè)字符,則PMT表中就有 j 個(gè)數(shù)值。其中第一個(gè)數(shù)值總為0。

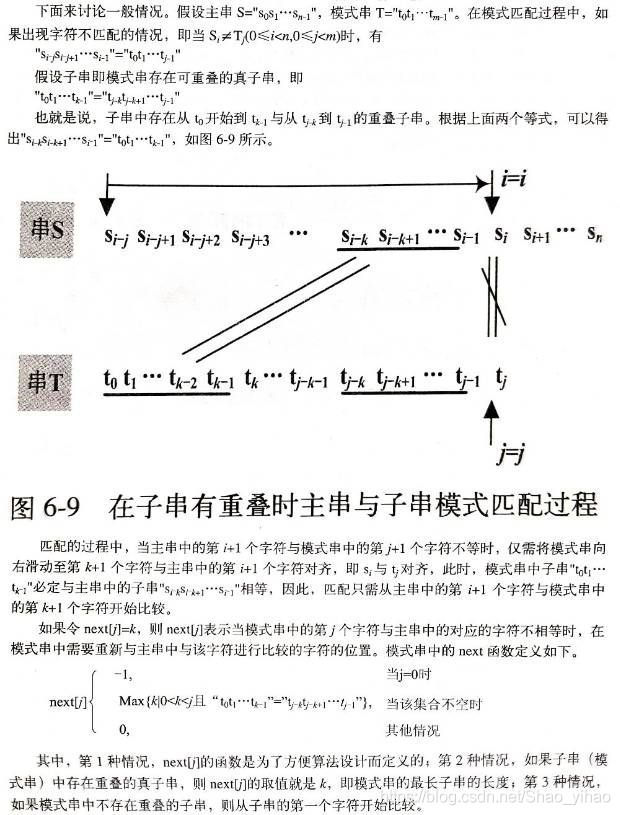
int index_KMP(SeqString S, SeqString T, int begin)//從S的第begin位(下標(biāo))開始進(jìn)行匹配判斷
{
int i = begin, j = 0;
while (i < S.length && j < T.length)
{
if (j == -1 || S.ch[i] == T.ch[j])
{
i ++;
j ++;
}
else j = next[j];//即PMT[j-1]
}
if (j == T.length) return i - T.length; //匹配成功,則返回該模式串在主串中第一次出現(xiàn)的位置下標(biāo)
else return -1;
}
那么該如何求出next數(shù)組呢?

其實(shí),求next數(shù)組的過程完全可以看成字符串匹配的過程,即以模式字符串為主字符串,以模式字符串的前綴為目標(biāo)字符串,一旦字符串匹配成功,那么當(dāng)前的next值就是匹配成功的字符串的長度。
具體來說,就是從模式字符串的第一位(注意,不包括第0位)開始對自身進(jìn)行匹配運(yùn)算。 在任一位置,能匹配的最長長度就是當(dāng)前i位置的next值。如下圖所示。
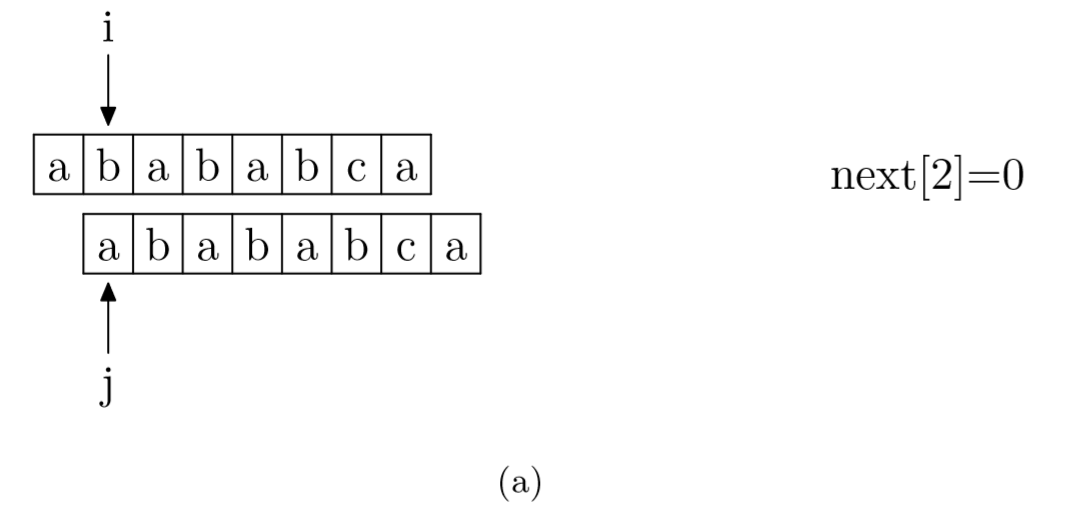
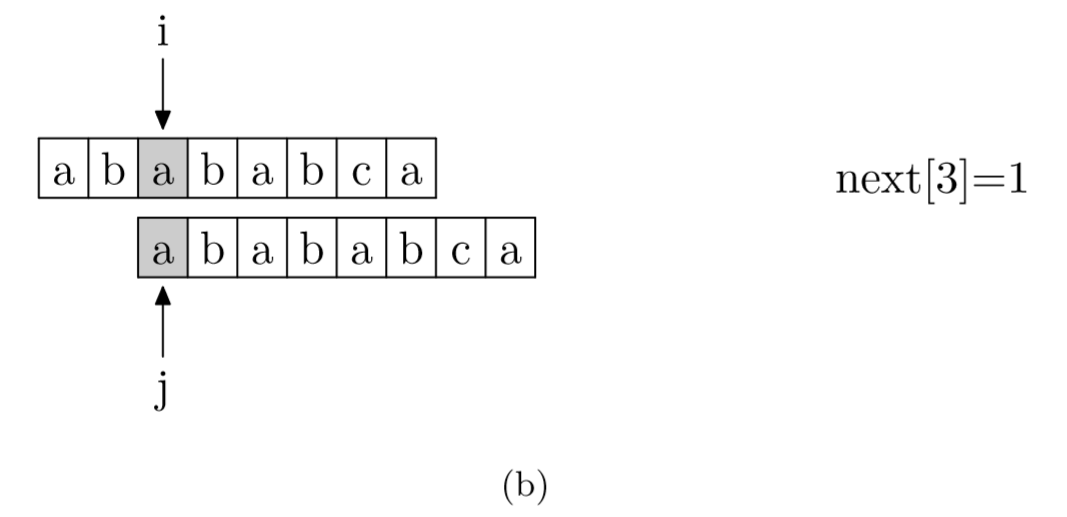
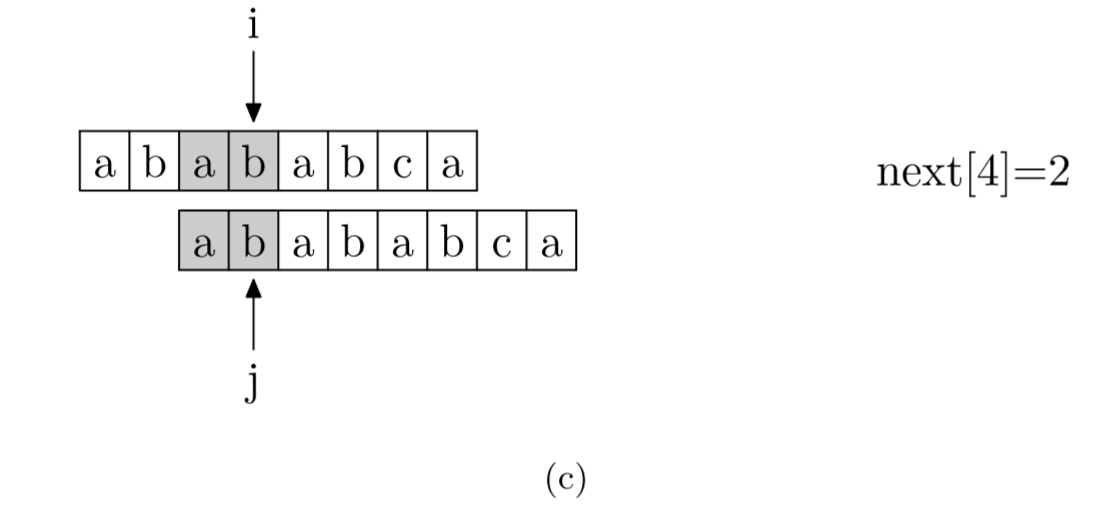
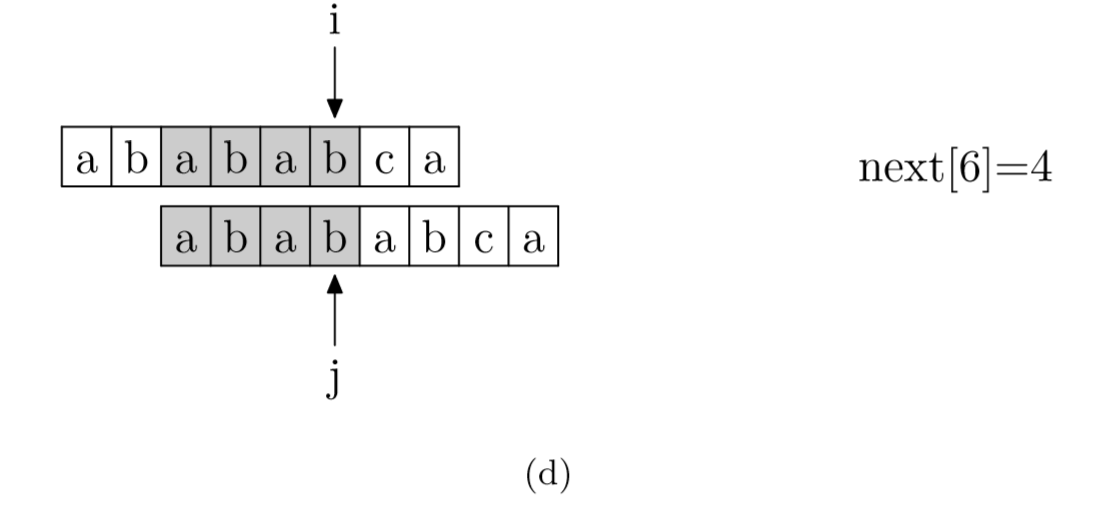
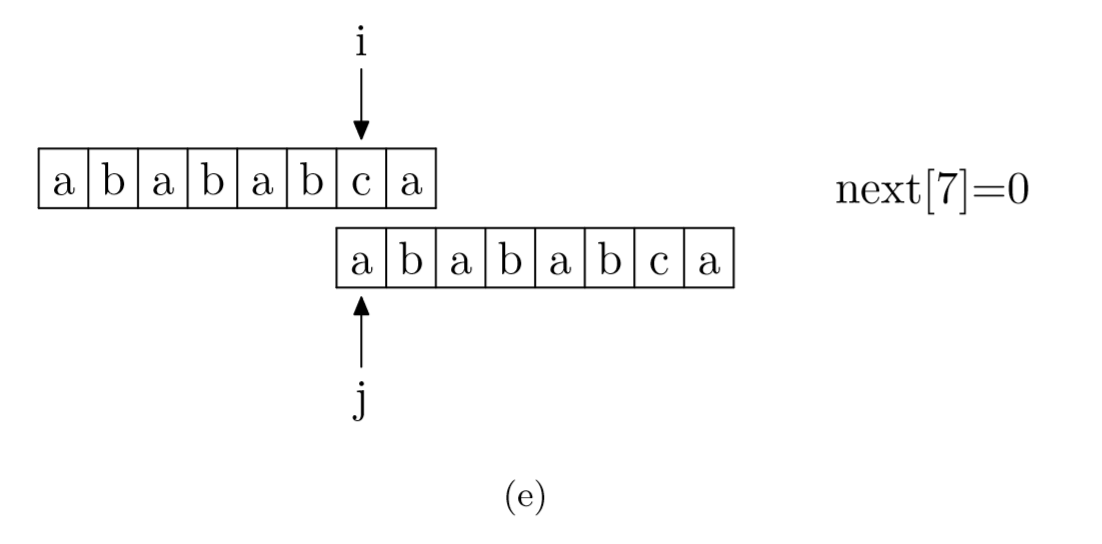
void GetNext(SeqString T, int next[])
{
next[0] = -1;
int j = 0, k = -1;//起始時(shí)k落后j一位
while (j < T.length)//j遍歷一遍模式串,對于每個(gè)字符得到該位置的next數(shù)組的值
{
if (k == -1 || T.ch[j] == T.ch[k])
{
j ++;
next[j] = k + 1;//將j視為指向一個(gè)子串(后綴)結(jié)束后的下一個(gè)字符,k指向一個(gè)子串(前綴)的最后一個(gè)字符,則這兩個(gè)子串的重疊部分的長度(k下標(biāo)從0開始)即PMT[j-1]的值
k ++;
/*也可以簡便地寫為(易記):
j ++;
k ++;
next[j] = k;
最簡單的形式為:
next[++ j] = ++ k;
*/
}
else k = next[k];//k回溯,即將第二個(gè)子串(右滑)(減小匹配的前綴長度)
}
}
即:
#include <stdio.h>
#include <string.h>
int next[10];//全局?jǐn)?shù)組
void GetNext(char T[])
{
int j = 0, k = -1;
next[0] = -1;
while (j < strlen(T))
{
if (k == -1 || T[j] == T[k])
{
j ++;
next[j] = k + 1;
k ++;
}
else k = next[k];
}
}
int index_KMP(char S[], char T[], int begin)//從S的第begin位(下標(biāo))開始進(jìn)行匹配判斷
{
int i = begin, j = 0;
while (i < strlen(S) && strlen(T))
{
if (j == -1 || S[i] == T[j])
{
i ++;
j ++;
}
else j = next[j];//即PMT[j-1]
}
if (j == strlen(T)) return i - strlen(T); //匹配成功,則返回該模式串在主串中第一次出現(xiàn)的位置下標(biāo)
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "cde";
GetNext(str2);
printf("%d", index_KMP(str1, str2, 0));
return 0;
}
求next數(shù)組的方法也可進(jìn)行優(yōu)化:
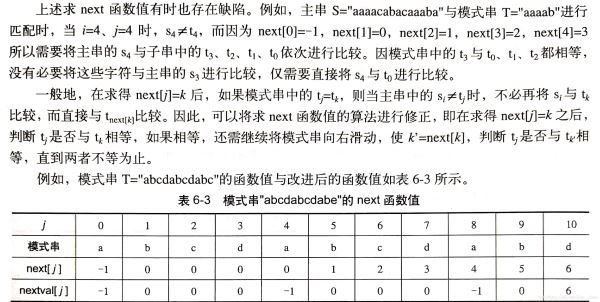
void GetNextVal(SeqString T, int nextval[])
{
nextval[0] = -1;
int j = 0, k = -1;
while (j < T.length)
{
if (k == -1 || T.ch[j] == T.ch[k])
{
j ++;
k ++;
if (T.ch[j] != T.ch[k])
nextval[j] = k;
else
nextval[j] = nextval[k];
}
else k = nextval[k];
}
}
即:
int nextval[10];//全局?jǐn)?shù)組
void GetNextVal(char T[])
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < strlen(T))
{
if (k == -1 || T[j] == T[k])
{
j ++;
k ++;
if (T[j] != T[k]) nextval[j] = k;
else nextval[j] = nextval[k];
}
else k = nextval[k];
}
}
int index_KMP(char S[], char T[], int begin)//從S的第begin位(下標(biāo))開始進(jìn)行匹配判斷
{
int i = begin, j = 0;
while (i < strlen(S) && strlen(T))
{
if (j == -1 || S[i] == T[j])
{
i ++;
j ++;
}
else j = nextval[j];
}
if (j == strlen(T)) return i - strlen(T); //匹配成功,則返回該模式串在主串中第一次出現(xiàn)的位置下標(biāo)
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "bcde";
GetNextVal(str2);
printf("%d", index_KMP(str1, str2, 0));
return 0;
}
KMP—yxc模板
字符串從數(shù)組下標(biāo)1開始存
#include <iostream>
using namespace std;
const int M = 1000010, N = 100010;
char S[M], p[N];
int ne[N]; //全局變量數(shù)組,初始化全為0
int main()
{
int m, n;
cin >> m;
for (int i = 1; i <= m; i ++) cin >> S[i];
cin >> n;
for (int i = 1; i <= n; i ++) cin >> p[i];//主串與模式串均由數(shù)組下標(biāo)1開始存儲
// 也可以簡寫為 cin >> m >> S + 1 >> n >> p + 1;
for (int i = 2, j = 0; i <= n; i ++)//求模式串各字符處的next值,即求串p[1~i]的前后綴最大交集的長度
{ //由于字符串由下標(biāo)1開始存儲,next[i]+1也是模式串下次比較的起始下標(biāo)
while (j && p[i] != p[j + 1]) j = ne[j];//記錄的最大交集的長度減小,直到為0,表示p[1~i]前后綴無交集
if (p[i] == p[j + 1]) j ++;//該位匹配成功
ne[i] = j;//j即該位的ne值
}
for (int i = 1, j = 0; i <= m; i ++)//遍歷一遍主串
{
while (j && S[i] != p[j + 1]) j = ne[j];//不匹配且并非無路可退,則j后滑。j==0意味著當(dāng)前i所指的字符與模式串的第一個(gè)字符都不一樣,只能等該輪循環(huán)結(jié)束i++,之后再比較
if (S[i] == p[j + 1]) j ++;//該位匹配成功
if (j == n)//主串與模式串匹配成功
{
cout << i - n << ' ';//匹配時(shí),輸出 模式串首元素在主串中的下標(biāo)
j = ne[j];//j后滑,準(zhǔn)備繼續(xù)尋找下一個(gè)匹配處
}
}
return 0;
}
字符串從數(shù)組下標(biāo)為開始存
const int N = 1000010;
char s[N], p[N];
int ne[N];
int main()
{
int n, m;
cin >> m >> p >> n >> s;
ne[0] = -1;//ne[0]初始化為-1
for (int i = 1, j = -1; i < m; i ++ )//從模式串的第2位2開始求next值
{
while (j != -1 && p[j + 1] != p[i]) j = ne[j];
if (p[j + 1] == p[i]) j ++ ;
ne[i] = j;
}
for (int i = 0, j = -1; i < n; i ++ )//遍歷一遍主串
{
while (j != -1 && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m - 1)//掃描到模式串結(jié)尾,說明匹配完成
{
cout << i - j << ' ';
j = ne[j];
}
}
return 0;
}
總結(jié)
本篇文章就到這里了,希望能夠給你帶來幫助,也希望您能夠多多關(guān)注html5模板網(wǎng)的更多內(nèi)容!
