堆(優(yōu)先隊(duì)列)是一種典型的數(shù)據(jù)結(jié)構(gòu),其形狀是一棵完全二叉樹,一般用于求解topk問題。根據(jù)雙親節(jié)點(diǎn)大于等于孩子節(jié)點(diǎn)或雙親節(jié)點(diǎn)小于等于孩子節(jié)點(diǎn),可分為大頂堆和小頂堆,本文實(shí)現(xiàn)大頂堆。
根據(jù)大頂堆的定義,大頂堆的雙親節(jié)點(diǎn)大于等于其孩子節(jié)點(diǎn),堆頂元素最大,對于每一個子樹都是一個大頂堆,則從最后一個雙親節(jié)點(diǎn)進(jìn)行調(diào)整為大頂堆,一直到根節(jié)點(diǎn),則可構(gòu)建一個大頂堆。
我們這里采用數(shù)組去存儲,以heap={3,2,1,5,6,4}為例,需要一個init(int[] heap)初始化方法,從最后一個雙親節(jié)點(diǎn)開始將heap逐漸調(diào)整為大頂堆,其中需要使用到adjust(int[] heap, int i, int end)方法。
調(diào)整過程:從最后一個雙親節(jié)點(diǎn)出發(fā),如果以當(dāng)前雙親節(jié)點(diǎn)為根的樹不符合大頂堆,則進(jìn)行調(diào)整。
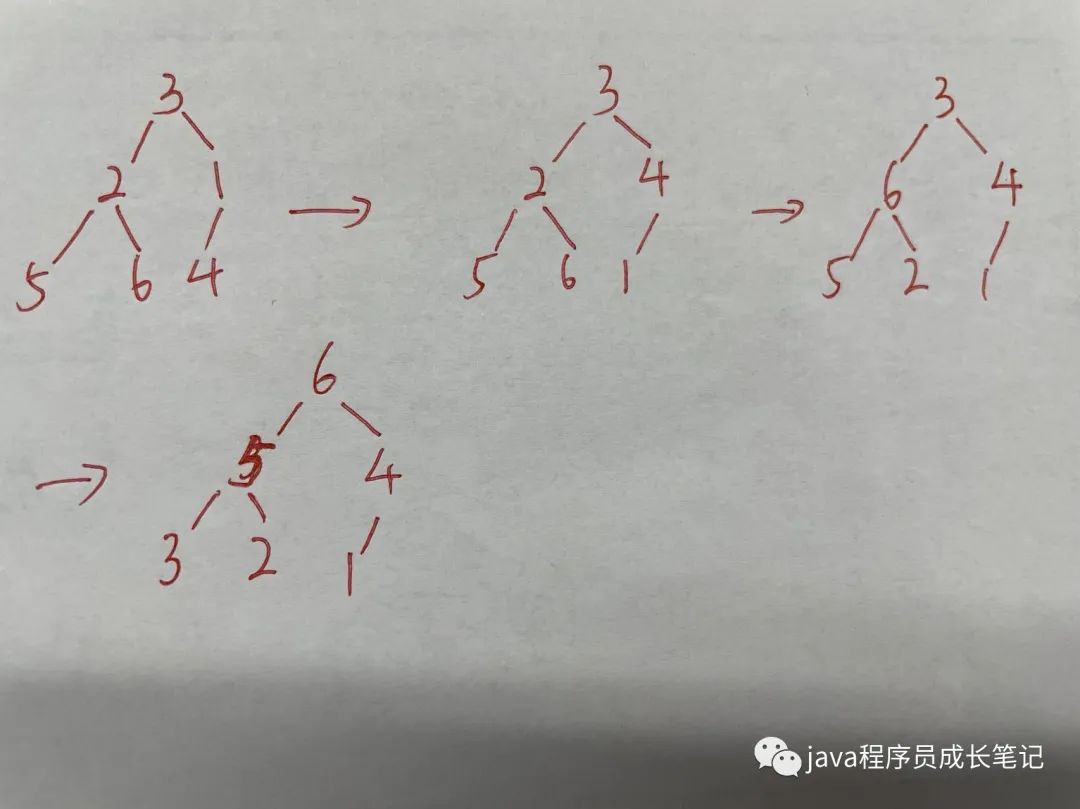
代碼實(shí)現(xiàn)如下:
public void init(int[] heap) {
//從最后一個雙親節(jié)點(diǎn)開始調(diào)整
//逐漸往上進(jìn)行調(diào)整
for (int i = heap.length / 2 ; i > 0 ; i-- ) {
this.adjust(heap, i, heap.length);
}
}
public void adjust(int[] heap, int i, int end) {
int j = i << 1;
while (j <= end) {
//找到兩個孩子節(jié)點(diǎn)z中較大的節(jié)點(diǎn)
if (j < end && heap[j - 1] < heap[j]) {
j = j + 1;
}
//如果較大節(jié)點(diǎn)還小于根節(jié)點(diǎn),則以當(dāng)前節(jié)點(diǎn)為根節(jié)點(diǎn)的
//二叉樹已經(jīng)是大頂堆,不需要進(jìn)行調(diào)整
if (heap[i - 1] > heap[j - 1]) {
break;
}
//進(jìn)行調(diào)整,將當(dāng)前節(jié)點(diǎn)換到較大位置,再從當(dāng)前位置進(jìn)行調(diào)整
int temp = heap[i - 1];
heap[i - 1] = heap[j - 1];
heap[j - 1] = temp;
i = j;
j = i << 1;
}
}構(gòu)建好了大頂堆之后,我們?nèi)绾吻蟮胻opk呢,此時堆頂元素為top1,我們只需要將top1元素拿走,將剩下元素調(diào)整為大頂堆,k次之后即可得到topk。
具體過程:我們將堆頂元素與最后一個元素進(jìn)行交換,然后將堆頂?shù)降箶?shù)第二個元素進(jìn)行調(diào)整,依次類推。
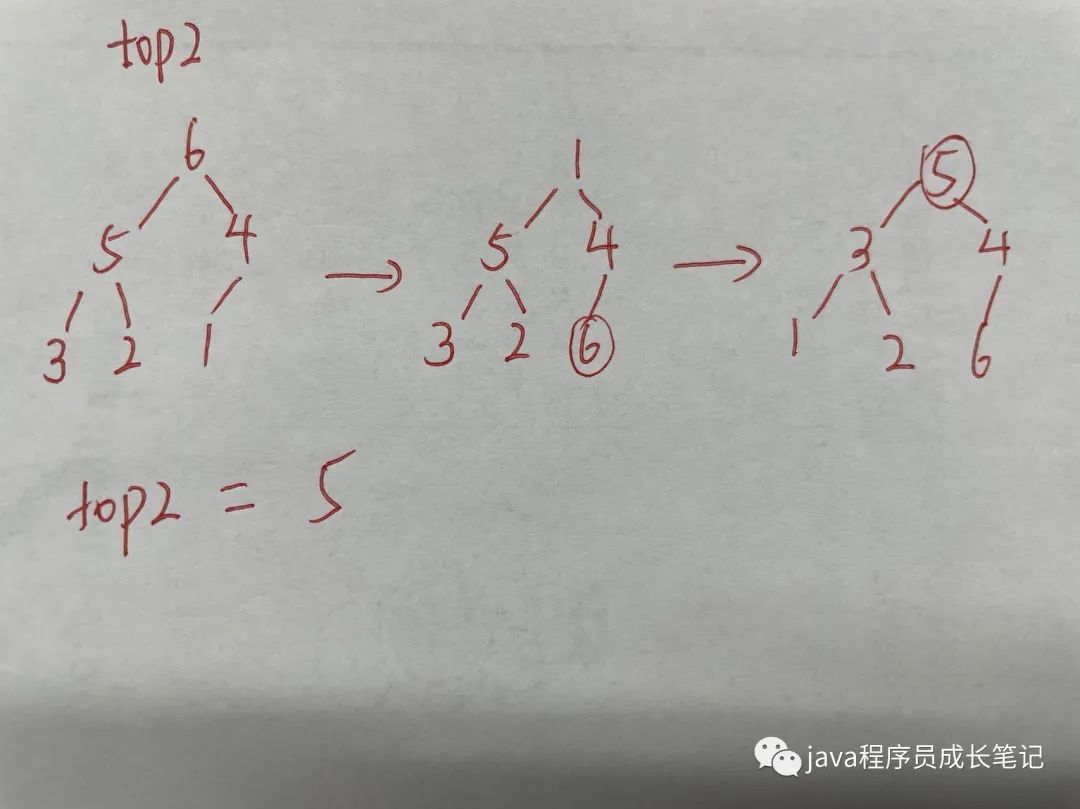
以leetcode215數(shù)組中第k個最大元素為例:
給定整數(shù)數(shù)組 nums 和整數(shù) k,請返回數(shù)組中第 k 個最大的元素。
請注意,你需要找的是數(shù)組排序后的第 k 個最大的元素,而不是第 k 個不同的元素
public int findKthLargest(int[] nums, int k) {
this.init(nums);
//找到第k大的數(shù)
int end = nums.length;
while (k > 1) {
//將當(dāng)前堆頂元素放到末尾,進(jìn)行堆調(diào)整
int temp = nums[0];
nums[0] = nums[end - 1];
nums[end - 1] = temp;
end = end - 1;
-- k;
this.adjust(nums, 1, end);
}
return nums[0];
} 
此外,Java本身提供了優(yōu)先隊(duì)列集合類,但是對于這個題目效率不如自己實(shí)現(xiàn)的高
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k);
for (int num : nums) {
if (priorityQueue.size() == k) {
if (num > priorityQueue.peek()) {
priorityQueue.poll();
priorityQueue.add(num);
}
continue;
}
priorityQueue.add(num);
}
return priorityQueue.poll();
}
到此這篇關(guān)于Java數(shù)據(jù)結(jié)構(gòu)之堆(優(yōu)先隊(duì)列)的實(shí)現(xiàn)的文章就介紹到這了,更多相關(guān)Java 堆內(nèi)容請搜索html5模板網(wǎng)以前的文章希望大家以后多多支持html5模板網(wǎng)!
